«Big O notation» o como obtener mayor eficiencia en tus algoritmos.

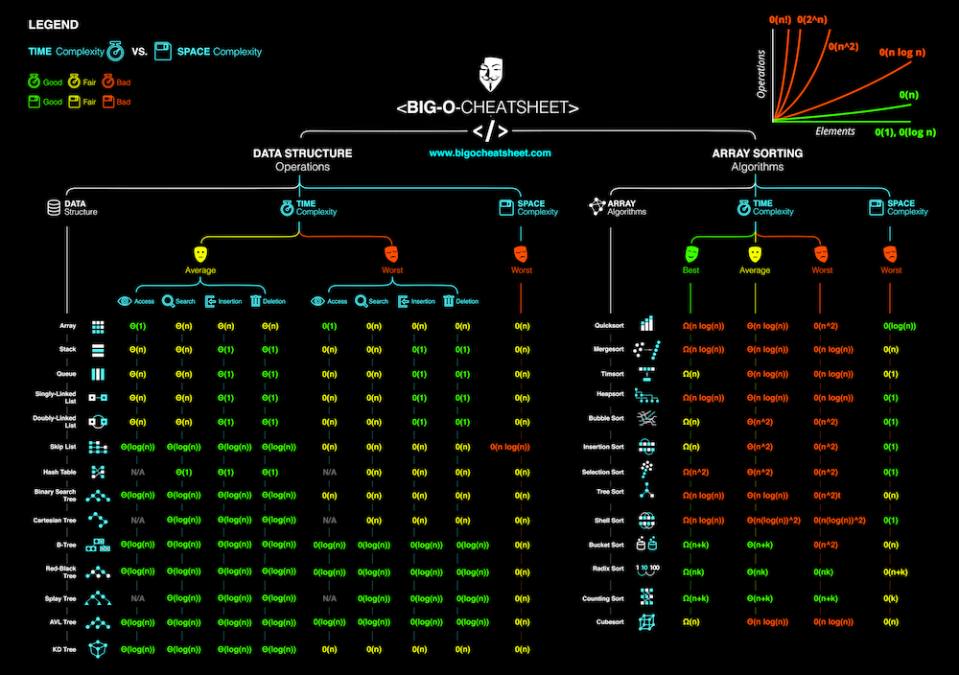
Imagen: Esquema de estructuras de datos y conocidos algoritmos para operar sobre las mismas.

Esta es mi primera entrada del blog. He pensado que una buena forma de empezar con él, sería escribir acerca de algo que considero importante en la calidad del software.

Para el que aún no sepa de lo que estoy hablando, voy a escribir acerca de Big O notation o el orden de complejidad de un algoritmo. Voy a tratar de hacerlo evitando al máximo las definiciones matemáticas formales que puedas encontrar en sitios como Wikipedia, ya que trato de aportar valor, utilidad en tu día a día, ya sea en proyectos profesionales o personales.

Hoy voy a tratar de darte las claves para conocer qué complejidad computacional tienen tus algoritmos a la hora de atravesar una estructura de datos y sobre todo como impacta el cómo lo haces en su escalabilidad.

Seguramente a estas alturas puedas estar pensando que soy una suerte de «mago teórico» y no voy a enseñarte nada nuevo, así como no lo aprendes cuando lees respuestas complejas de algoritmia en Stack Overflow con miles de «upvotes».

Para ser honesto, déjame decirte que seguramente a corto plazo no notes una «mejora mágica» en el rendimiento del software que estás desarrollando, si tratas de aplicar todo lo que cuento aquí, pero sí que lo notarás a medio y largo plazo.

La escalabilidad está muy ligada al concepto de «resiliencia» o en cuanto a este área del conocimiento, a la capacidad de un software de adaptarse a cambios en su volumen, en su crecimiento, sin perder calidad o fluidez.

Esta notación indica el orden de complejidad en el cual se está ejecutando nuestro algoritmo a la hora de operar sobre una estructura de datos.

Existen ciertos tipos de estructuras de datos, que llevan asociado un orden de complejidad determinado a la hora de leer o escribir en ella, quizá pueda dejarme alguna en el tintero, cosa que espero poder solucionar mediante vuestro feedback.

O(1) – Tiempo constante. El camino más fácil.

Cuando nuestro algoritmo se ejecuta en una cantidad de tiempo constante, para una cantidad indeterminada de elementos en un conjunto de datos.

Podría resumirse en que solo realizaremos una operación para n entradas en nuestra estructura, sea n = 1 o n = 200 el tamaño de nuestro array, por ejemplo. Esto es en cristiano un coste muy bajo.

Estructuras que nos permiten este tipo de acceso:

Hash tables. Si estás en Java seguramente los conozcas como Mapas, cada lenguaje realiza su implementación basada en «direccionamiento abierto» (open adressing) o «encadenamiento separado» (separate chaining).
Diccionarios.

Un ejemplo sería el siguiente. Ejemplo extraído del libro The Imposters Handbook:

const sumContiguousArray = function(ary) {
//get the last item
const lastItem = ary[ary.length – 1];
//Gauss’s trick
return lastItem * (listItem + 1) / 2;
}
const nums = [1,2,3,4,5];
const sumOfArray = sumContiguousArray(nums);

Esta función recibe el array de números como argumento y calcula la suma de todos sus elementos sin necesidad de atravesarlo o iterarlo. Es decir, tenemos una operación independientemente del tamaño del array.

Esto es posible debido a la siguiente fórmula de Gauss:

S = n(n+1)/2;
5(5 + 1)/2 = 15

El resultado es 15, la suma de todos los elementos del array. Para poder lograr esto el array debe ser una secuencia de valores ordenada de 1 … n.

Esto no significa que este algoritmo sea el único que nos permita realizar una única operación independientemente del número de entradas del array, hay muchas otras soluciones que ya existen o que tú puedes idear para resolver tus problemas sin necesidad de iterar una estructura, en base a una decisión o criterio.

En este caso esa decisión, ha sido utilizar una fórmula que en base a unos requisitos cumplidos (orden del array, orden de los valores y sucesión), que permita obtener una solución sin necesidad de «buscarla», ya que nuestro problema es justamente que cada operación nos cuesta recursos y evita que nuestra aplicación escale de forma aceptable.

Esta decisión o criterio que reduce lo que aparentemente pudiese ser una operación de iteración sobre un array de orden O(n), se reduzca a O(1), una única operación independientemente del tamaño del array.

El orden de complejidad de nuestro algoritmo no variará por mucho que nuestro array pase a tener un millón de elementos (siempre será uno) y nuestra solución escalará perfectamente aunque el volumen de entradas aumente.

Otro típico ejemplo puede ser acceder a un item de un HashMap en Java o cualquier implementación de una Hash Table.

// Creating the map
Map<String, Integer> exampleMap = new Map<String, String>();

//Inserting elements in map. Name and age pair
exampleMap.put(«José», 25);

Integer yearsOld = exampleMap.get(«José»);
System.out.println(«Years old of José: » + yearsOld);

Como se ve, hemos podido acceder sin necesidad de iterar la estructura a un valor que conocemos en base a una clave, una clave que conocemos, con un valor semántico que conocemos. Tal como pasaría si hiciésemos lo siguiente en JS:

var arr = [1, 4, 5, 9]

console.log(«Última posición: » + (arr.lenght – 1) );

Evidentemente este tipo de ejemplos pueden resultar ridículos, pero pueden hacerte entender mejor cual es la idea del concepto del coste constante

En el último ejemplo, aunque tengamos 20 entradas más en el array, el orden de complejidad seguiría siendo O(1), seguiríamos accediendo siempre a la última posición del array mediante una única operación.

O(n) – Tiempo lineal. Una solución aceptable.

Cualquier operación que requiera de atravesar una estructura de datos, que requiera de una operación o «iteración» por entrada.

Esto suele darse en los típicos algoritmos de búsqueda de una ocurrencia o «match» en un array de la forma que usualmente tendemos a implementar, aunque puede mejorarse (no siempre), en base a una decisión que lo evite tal y como pasaba con la solución O(1).

Una implementación de un algoritmo de coste O(n) típica en JS:

var names = [«Alba», «Danny», «Manuel», «Roberto»];
var keySearched = «Manuel»;
var positionLocated = -1;

for (var record = 0; record < names.length; record++) {
if («keySearched» === names[record]) {
positionLocated = record;
}
}

console.log(«La clave buscada (» + keySearched + «), tiene el valor: » + names[positionLocated]);

Como podemos observar siempre realizaremos una operación por entrada del array, si tenemos 4 entradas como en nuestro caso, realizaremos cuatro operaciones o iteraciones; si tenemos 20 entradas, realizaremos 20 operaciones.

Esto es que nuestro algoritmo es de orden O(n), o lo que es lo mismo: escala linealmente.

O(n^2) – La fuerza bruta. Una solución no tan aceptable.

Esto lo hemos hecho todos más de una vez, yo el primero. Más de una vez nos hemos visto en la situación de tener que iterar un array de dos o más dimensiones en busca de un valor dado.

Esto que «a priori» puede parecernos una idea sencilla, cómoda, bien conocida y genial a todos los efectos, puede llevarnos a resultados no tan «geniales».

Veamos un ejemplo con código. Ejemplo extraído del libro The Imposters Handbook:

const hasDuplicates = function(num) {
// loop the list, our O(n) op
for(let i = 0; i < nums.length; i++) {
const thisNum = nums[i];
// loop the list again, the O(n^2) op
for(let j = 0; j < nums.length; j++) {
//make sure we’re not checking same number
if(j !== i) {
const otherNum = nums[j];
//if there’s an equal value, return
if(otherNum === thisNum)
return true;
}
}
}
//if we’re here, no dups
return false;
}
const nums = [1,2,3,4,5,5];
hasDuplicates(nums);//true

Esta función recoge un array por parámetro y para cada una de sus entradas realiza una búsqueda para tratar de localizar duplicados, evitando que se tenga en cuenta la posición desde la que se busca el duplicado.

Esto es una solución con un coste altísimo, ya que aunque en este caso aunque tengamos como resultado un total de 6 * 6 = 36 operaciones, si nuestro conjunto de datos escala a 1000, tendríamos un coste de 1000 * 1000 = 1000000. Esto es, un millón de operaciones que pueden ser a modo de ejemplo:

Un millón de consultas a una API REST por la que se nos puede estar cobrando según su segmentación.
Un millón de consultas a base de datos que puede ralentizar la velocidad con la que nuestra base de datos responde a peticiones de otros servicios de nuestra aplicación o de otra aplicación.

Además del evidente aumento de tiempo de ejecución y respuesta de la aplicación, que resultará en que quizá nuestros clientes, si nuestro algoritmo reside en una aplicación web, se vayan a la competencia. Más adelante veremos como podemos reducir este coste siempre y cuando el array esté ordenado (para este ejemplo), para lo cual necesitarás leer la sección contigua del artículo.

O(log n) – Divide y vencerás.

Este tipo de orden de complejidad se basa en la definición formal matemática de que una ecuación exponencial es la equivalencia inversa a un logaritmo y viceversa. Esto es tal que:

Log2(128) = 7 => 2^7 = 128

Esto puede verse fácilmente en el algoritmo de búsqueda binaria, que necesita de un array ordenado para poder funcionar, debido a la estructura de datos jerárquica en la que se basa, el «Binary Tree», pero que puede implementarse para operar sobre un array.

Os dejo con unos vídeo explicativos acerca de este algoritmo:

Binary Search

El Árbol Binario de Búsqueda | | UPV

Básicamente consiste en ir partiendo el array en trozos de dos e ir descartando el trozo que no queremos. ¿Cómo sabemos qué trozo no queremos? Una estrategia simple, sería preguntar si el número que buscamos es igual o menos que el número buscado y tomar una decisión sobre que sección del array continuar reduciendo.

Aquí puede verse gráficamente como se va segmentando el array, siempre por la mitad de este, o por una aproximación de la mitad:

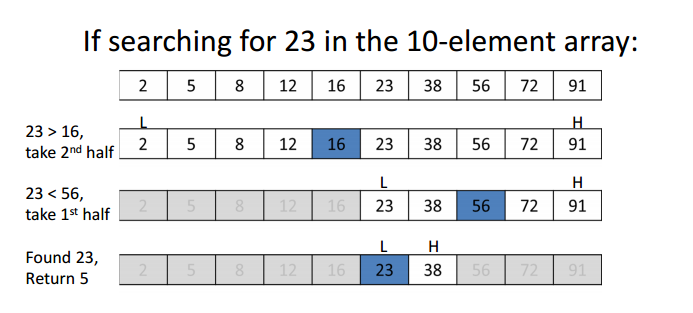
De esta forma, para el siguiente array dado:

var arr = [1, 2 , 8, 9, 10];

Mediante una clásica implementación que consistiese en recorrer el array por completo, tendría un coste de O(n). Para este caso del array que he ejemplificado O(5), es decir, 5 operaciones. Sin embargo, si implementamos el algoritmo de «Búsqueda Binaria» o «Binary Search», lograremos reducir el coste a un orden O(log n), es decir: log2(5), que da un resultado de O(3), es decir, tres operaciones en lugar de 5. La base dos del logaritmo es debido a que siempre se realiza una división en dos trozos, ten siempre esto en mente.

Aunque realmente el logaritmo no da tres, si no dos con algún decimal, necesitamos realizar una aproximación en base 2 que es aquello que manejamos usualmente como desarrolladores, para estar seguros de que encontraremos el valor en ese rango, que nos dejaría un valor entre 2^2 = 4 y 2^3 = 8, un valor entre 4 y 8, como buscábamos 5, lo hemos encontrado dentro del intervalo mencionado.

Reduciendo O(n^2) a O(n log n) – Evitando la fuerza bruta.

Si has llegado hasta aquí y has sido paciente, hemos llegado a como optimizar el problema de la fuerza bruta. Si también te has enterado de que el coste de un loop es O(n), te será sencillo imaginar que O(n^2) es un loop anidado, es decir, un bucle anidado en otro bucle.

var arr = [[2,4,2], [2,1,6], [6,4,2]];
var sum = 0;

for (var i = 0; i < arr.lenght; i++) {
for(var j = 0; j < arr[i].length; j++) {
sum += arr[i][j];
}
}

Esta implementación tan típica que comentábamos antes es una función con una complejidad que deberíamos evitar, debido al coste computacional que requeriría a un volumen mayor de entradas en el array.

En ciertos casos podremos reducir el coste computacional de una función de orden O(n^2) . Vamos a ver el caso de reducción sobre un algoritmo de búsqueda de duplicados de una sola dimensión, que requeriría de un bucle anidado como el mostrado arriba en soluciones comunes, pero al que podemos reducir el coste para la segunda iteración (la función searchFor) de un coste O(n) a un coste O(log n) basándonos en el algoritmo de búsqueda binaria para encontrar el posible duplicado, de esta forma tendremos un coste total de O(n log n).

En definitiva, hemos conseguido reducido el coste y esta solución escalará mejor ante posibles aumentos de entradas en el array, que una solución de fuerza bruta.

Ejemplo extraído del libro The Imposters Handbook:

const nums = [1,2,3,4,5];
const searchFor = function(items, num){
//use binary search!
//if found, return the number. Otherwise…
//return null. We’ll do this in a later chapter.
}
const hasDuplicates = function(nums) {
for(let num of nums){
//let’s go through the list again and have a look
//at all the other numbers so we can compare
if(searchFor(nums,num)) {
return true;
}
}
//only arrive here if there are no dups
return false;
}

Yendo un poco más lejos. Reduciendo el orden O(n log n) a O(n)

Siempre debemos tratar de reducir el orden de complejidad de nuestras funciones la máximo posible, estableciendo criterios basados en cosas que nosotros conozcamos. Algo que sabemos, es que si tenemos un array ordenado, en base a su longitud, podríamos saber mediante el truco de Gauss el resultado de la suma de sus elementos. Siempre y cuando estos elementos estén ordenados y vayan del orden de 1 … n.

Una vez obtenemos el resultado de lo que debería ser la suma de los items (el array supuestamente correcto), se lo restamos al resultado de sumar los elementos del que llamaremos array real, esto es, que tendremos que iterar el array real para conocer el valor de la suma de cada uno de sus elementos, O(n).

Sin embargo, lo que antes requería de una segunda iteración mediante el uso de un algoritmo de búsqueda binaria de orden O(log n), ahora requiere una simple operación que supone algo que sabemos que va a funcionar en base a nuestra capacidad de observación y a que es una fórmula demostrada de Gauss.

De forma que al final obtendríamos un algoritmo de búsqueda de duplicados que:

Mediante fuerza bruta tenía un coste de orden O(n^2).
Mediante su reducción a través de un algoritmo de búsqueda binaria tenía un coste O(n log n)
Que hemos conseguido reducir a un algoritmo de orden O(n * 1), es decir, O(n). Hemos pasado de un algoritmo con un orden que escalaba exponencialmente a uno que lo hace de forma lineal.

Ejemplo extraído del libro The Imposters Handbook:

const findDuplicate = function(ary){
//sum what we’re given
let actualSum = 0;

//our O(n) scan
ary.forEach(x => actualSum += x);

//get the last item
const lastItem = ary[ary.length – 1];

//create a new array
const shouldBe = lastItem * (lastItem + 1) / 2;

return actualSum – shouldBe;
}
const nums = [1,2,3,4,4,5];
const duplicate = findDuplicate(nums);

Te sugiero si quieres comparar el coste de un algoritmo de orden O(n^2) contra uno de orden O(n), que visites la siguiente web, donde puedes ver gráficamente la consecuencia de como escala un algoritmo según su orden. Viene bastante claro.

Know Thy Complexities!

¡Gracias por leer mi artículo!